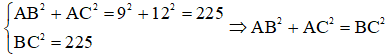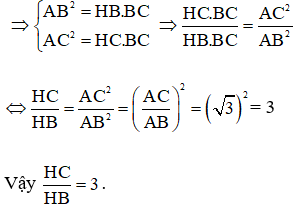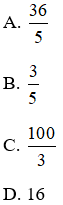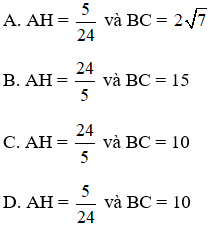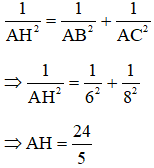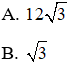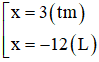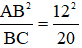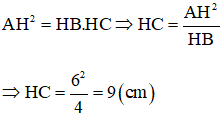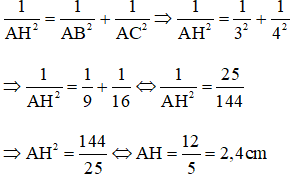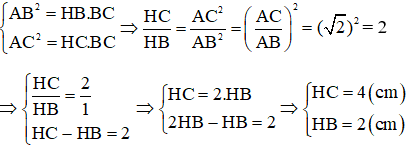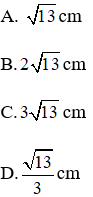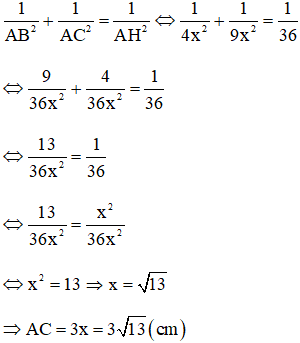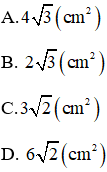Cách tính độ dài cạnh góc vuông trong tam giác vuông cực hay | Toán lớp 9

Cách tính độ dài cạnh góc vuông trong tam giác vuông cực hay

Với Cách tính độ dài cạnh góc vuông trong tam giác vuông cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính độ dài cạnh góc vuông trong tam giác vuông từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Tải xuống

A. Phương pháp giải

• Xác định vị trí cạnh huyền

• Áp dụng hệ thức về cạnh hoặc đường cao đã được học.

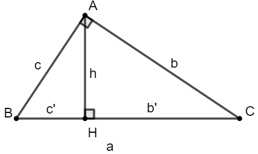
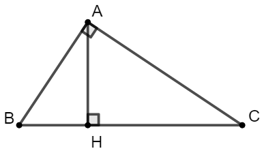
Cho ΔABC, 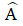= 90⁰, AH ⊥ BC, BC = a, AB = c, AC = b, AH = h thì:

+) BH = c’ được gọi là hình chiếu của AB trên cạnh huyền BC

+) CH = b’ được gọi là hình chiếu của AC trên cạnh huyền BC

Khi đó ta có các hệ thức về cạnh và đường cao trong tam giác vuông:

1) b² = ab'; c² = ac'

2) h² = b'c'

3) ha = bc

4)

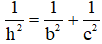
5) a² = b² + c²( Định lý Pytago)

B. Ví dụ minh họa

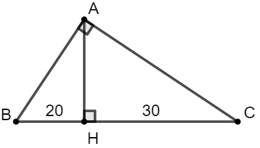
Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH, biết HB = 20cm, HC = 30cm. Tính AB, AC, AH.

Bài giải:

Ta có: BC = BH + HC = 20 + 30 = 50 (cm)

Áp dụng hệ thức lượng trong tam giác vuông ABC có đường cao AH:

+) AB² = BH.BC = 20.50 = 1000 ⇒ AB = 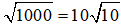(cm)

+) AC² = CH.CB = 30.50 = 1500 ⇒ AC = 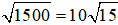(cm)

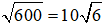
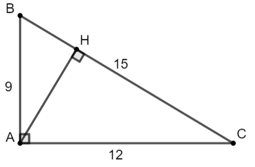
+) AH² = BH.CH = 20.30 = 600 ⇒ AH = (cm)

Ví dụ 2: Cho tam giác ABC có AB = 9cm; AC = 12cm; BC = 15cm, đường cao AH. Tính độ dài AH.

Bài giải:

Xét tam giác ABC có:

⇒ Tam giác ABC vuông tại A có đường cao AH (Định lý Py - ta - go đảo)

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AH.BC = AB.AC ⇒ AH.15 = 9.12 ⇒ AH = 7,2 cm

Ví dụ 3: Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AC : AB = 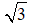. Tỉ số HC : HB bằng

Bài giải:

Áp dụng hệ thức lượng trong tam giác vuông ABC có đường cao AH:

C. Bài tập trắc nghiệm

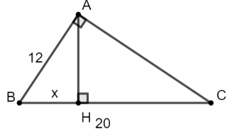
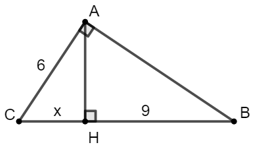
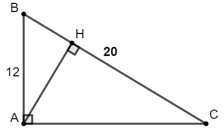
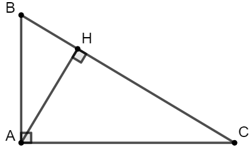
Bài 1: Giá trị của x trong hình bên là bao nhiêu biết BC = 20, AB = 12

Bài giải:

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AB² = BH.BC

⇔ 12² = x.20

⇒ x =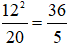

Đáp án A.

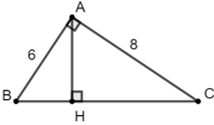
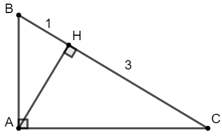
Bài 2: Tìm AH, BC với các giá trị như hình bên.

Bài giải:

+) Áp dụng định lý Pytago cho tam giác vuông ABC ta có:

BC² = AB² + AC²

⇒ BC² = 6² + 8² = 100 ⇒ BC = 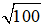= 10

+) Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH:

Đáp án C.

Bài 3: Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 6cm, BH = 9cm. Tính độ dài BC.

C. 3

D. 12

Bài giải:

Đặt HC = x (x > 0)⇒ BC = x + 9

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AC² = BC.HC

⇔ 6² = (x + 9). x

⇔ x² + 9x - 36 = 0

⇔ x² + 12x - 3x - 36 = 0

⇔ x(x + 12) - 3(x + 12) = 0

⇔ (x - 3)(x + 12) = 0

⇒

Vậy BC = BH + CH = 9 + 3 = 12cm

Đáp án D.

Bài 4: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 20cm. Tính HC.

A. 6,4cm

B. 7,2cm

C. 12,8cm

D. 16,4cm

Bài giải:

Theo hệ thức lượng trong tam giác vuông ta có:

AB² = HB.BC ⇒ HB =

⇒ HB = 7,2cm

⇒ HC = BC = HB = 20 - 7,2 = 12,8cm

Đáp án C.

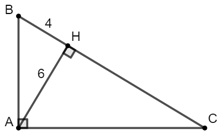
Bài 5: Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 6cm, HB = 4cm. Tính BC.

A. 10cm

B. 11cm

C. 12 cm

D. 13 cm

Bài giải:

Áp dụng hệ thức lượng trong tam giác vuông ta có:

⇒ BC = BH + HC = 4 + 9 = 13 (cm)

Đáp án D.

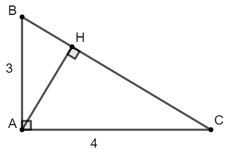
Bài 6: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính AH.

A. 5,6 cm

B. 2,4 cm

C. 3,6 cm

D. 3,4 cm

Bài giải:

Theo hệ thức lượng trong tam giác vuông ABC ta có:

Đáp án B.

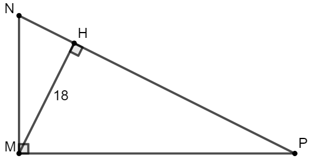
Bài 7: Cho ΔMNP vuông tại M, đường cao MH = 18cm. Biết HN : HP = 1 : 4. Tính độ dài cạnh huyền NP.

A. 36 cm

B. 45 cm

C. 54 cm

D. 63 cm

Bài giải:

Gọi HN = x (x > 0) thì HP = 4x

Theo hệ thức lượng trong tam giác vuông ta có:

MH² = HN.HP

⇔ 18² = x.4x

⇔ 4x² = 324

⇔ x² = 81

⇔ x = 9 (cm)

⇒ HN = 9 cm và HP = 4x = 4.9 = 36 cm

Vậy NP = HN + HP = 9 + 36 = 45 cm

Đáp án B.

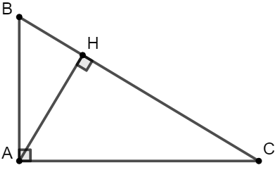
Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AC : AB = 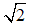và HC - HB = 2cm. Độ dài HC bằng:

A. 4 cm

B. 2 cm

C. 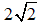cm

D. 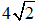cm

Bài giải:

Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:

Đáp án A.

Bài 9: Cho tam giác ABC vuông tại A có AB : AC = 2 : 3 và đường cao AH bằng 6cm. Khi đó độ dài đoạn thẳng AC bằng:

Bài giải:

Gọi AB = 2x (x > 0) thì AC = 3x

Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:

Đáp án C.

Bài 10: Cho tam giác ABC vuông ở A, đường cao AH. Biết HC = 3cm; HB = 1cm. Tính diện tích tam giác ABC.

Bài giải:

Xét tam giác ABC vuông ở A có đường cao AH:

+) AH² = HB.HC( Hệ thức lượng trong tam giác)

Đáp án B.