Các dạng bài tập Đường thẳng song song và đường thẳng cắt nhau chọn lọc | Toán lớp 9

Các dạng bài tập Đường thẳng song song và đường thẳng cắt nhau chọn lọc

Với Các dạng bài tập Đường thẳng song song và đường thẳng cắt nhau chọn lọc Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đường thẳng song song và đường thẳng cắt nhau từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

• Lý thuyết Đường thẳng song song và đường thẳng cắt nhau Xem chi tiết
• Dạng 1: Cách xác định hai đường thẳng song song, cắt nhau, vuông góc Xem chi tiết
• Dạng 2: Viết phương trình đường thẳng song song với đường thẳng Xem chi tiết
• Dạng 3: Viết phương trình đường thẳng vuông góc với đường thẳng Xem chi tiết
• Bài tập Đường thẳng song song và đường thẳng cắt nhau Xem chi tiết

Cách xác định hai đường thẳng song song, cắt nhau, vuông góc

Phương pháp giải

Cho hai đường thẳng:

    (d₁ ): y = ax + b (a ≠ 0)

    (d₂ ): y = a'x + b' (a' ≠ 0)

        + (d₁ ) // (d₂ ) ⇔ a = a'; b ≠ b'

        + (d₁ ) ≡ (d₂ ) ⇔ a = a'; b = b'

        + (d₁ ) cắt (d₂ ) ⇔ a ≠ a'

        + d₁ ⊥ d₂ ⇔ a.a' = -1.

Ví dụ minh họa

Ví dụ 1: Hãy chỉ ra các cặp đường thẳng song song và vuông góc trong các đường thẳng sau:

    d₁: y = 2x + 3

    d₄: y = 0,5x - 3

    d₅: y = 5 + 2x

    d₆: 7 - 2x

Hướng dẫn:

    Hai cặp đường thẳng song song là:

    d₁ // d₅ vì a = a' = 2; b ≠ b' (3 ≠ 5)

    d₂ // d₄ vì a = a' = 0,5; b ≠ b' (2 ≠ -3)

    Bốn cặp đường thẳng vuông góc với nhau là: d₁ ⊥ d₃; d₂ ⊥ d₆; d₃ ⊥ d₅; d₄ ⊥ d₆ vì đều có a.a' = -1.

Ví dụ 2: Chứng tỏ rẳng hai đường thẳng sau luôn cắt nhau với mọi giá trị của m

    a) (d₁ ): y = (m² - 4m + 5)x + 1 và (d₁ ): y = (-x + m)/2

    b) (d₃ ): y = (m² + 1)x + 2018 và (d₄ ): y = -mx + 2012

Hướng dẫn:

    a) Xét (d₁ ) có a = m² - 4m + 5 = (m - 2)² + 1 > 0

    (d₂ ) có a' = (-1)/2 < 0

    ⇒ a ≠ a' với mọi m nên (d₁ ) luôn cắt (d₂ )

    b) Xét (d₃ ) có a = m² + 1

    (d₄ ) có a' = -m

    Ta có: a - a' = m² + 1 + m = (m + 1/2)² + 3/4 > 0 ∀m

    ⇒ a ≠ a' với mọi m nên (d₃ ) luôn cắt (d₄ )

Bài tập vận dụng

Bài 1: Tìm ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các đường thẳng sau:

    a) y = √3x - 1 (1)        b) y = 2 - x (2)

    c) y = -0,3x (3)        d) y = -0,3x - 1 (4)

    e) y = 3 + √3x (5)        f) y = -x + 3 (6)

Bài 2: Cho hai hàm số bậc nhất y = 2x + 3k và y = (2m + 1)x + 2k - 3

    Tìm điều kiện đối với m và k để đồ thị của hai hàm số là:

    a) Hai đường thẳng cắt nhau

    b) Hai đường thẳng song song

    c) Hai đường thẳng trùng nhau.

Hướng dẫn giải và đáp án

Hướng dẫn:

Bài 1:

    Các cặp đường thẳng cắt nhau là: (1) và (2); (1) và (3); (1) và (4)

    Các cặp đường thẳng song song là: 1) và (5); (2) và (6); (3) và (4)

Bài 2:

    y = 2x + 3k và y = (2m + 1)x + 2k - 3

    a) Hai đường thẳng trên cắt nhau

    ⇔ 2m + 1 ≠ 2 ⇔ m ≠ 1/2

    b) Hai đường thẳng trên song song với nhau

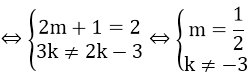
    c) Hai đường thẳng trên trùng nhau

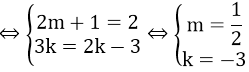
Cách Viết phương trình đường thẳng song song với đường thẳng

Phương pháp giải

    Viết phương trình đường thẳng đi qua một điểm và song song với một đường thẳng cho trước: Gọi phương trình đường thẳng cần tìm là y = ax + b.

        + Sử dụng điều kiện hai đường thẳng song song với nhau để xác định hệ số a.

        + Với a tìm được, sử dụng điều kiện còn lại để xác định tung độ gốc b.

Ví dụ minh họa

Ví dụ 1:: Cho 2 đường thẳng (d₁ ): y = (2 - m² )x - m - 5

    (d₂ ): y = -2x + 2m + 1

    Tìm m để hai đường thẳng song song với nhau

Hướng dẫn:

    (d₁) // (d₂)

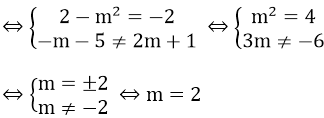
    Vậy với m = 2 thì hai đường thẳng trên song song với nhau.

Ví dụ 2: Cho đường thẳng (d): 2x + y – 3 = 0 và điểm M (-1; 1). Viết phương trình đường thẳng (d’) đi qua điểm M và song song với (d).

Hướng dẫn:

    Gọi phương trình đường thẳng (d’) là y = ax + b

    Ta có: (d): 2x + y – 3 = 0 hay y = -2x + 3.

    Vì (d) // (d’) nên a = -2 và b ≠ 3.

    Mặt khác, (d’) đi qua điểm M (-1; 1) nên 1 = a.(-1) + b ⇔ -a + b = 1

    ⇔ -(-2) + b = 1 ⇔ b = -1 (≠ 3).

    Vậy phương trình đường thẳng cần tìm là y = -2x - 1.

Bài tập vận dụng

Bài 1: Viết phương trình đường thẳng (d) đi qua điểm (-3; 4) và song song với đường thẳng (d'): y = 2x – 1

Bài 2: Cho M (0; 2), N(1; 0), P(-1; -1) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Viết phương trình đường thẳng AB.

Hướng dẫn giải và đáp án

Hướng dẫn:

Bài 1:

    Gọi phương trình đường thẳng (d) là y = ax + b

    Do (d) // (d’) nên a = 2; b ≠ -1.

    (d) đi qua điểm (-3; 4) nên: 4 = -3.a + b ⇔ 4 = -3.2 + b ⇔ b = 10.

    Vậy phương trình đường thẳng cần tìm là y = 2x + 10.

Bài 2:

    Gọi phương trình đường thẳng MN là: y = ax + b. Ta có:

    N(1; 0) ∈ MN ⇒ 0 = a.1 + b ⇔ a = -b

    M(0; 2) ∈ MN ⇒ 2 = a.0 + b ⇔ b = 2 ⇒ a = -2.

    Vậy phương trình đường thẳng MN là y = - 2x + 2.

    Vì M, N lần lượt là trung điểm của CB và CA nên MN là đường trung bình của tam giác ABC ⇒ MN // AB

    Vì AB // MN nên phương trình đường thẳng AB có dạng: y = -2x + b’ (b’ ≠ 2)

    Vì P (-1; -1) là trung điểm của đoạn thẳng AB nên đường thẳng AB đi qua P.

    ⇒ -1 = -2.(-1) + b' ⇒ b' = -3 (thỏa mãn)

    Vậy phương trình đường thẳng AB là y = -2x - 3.