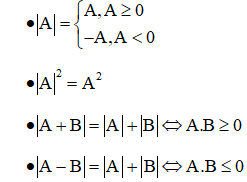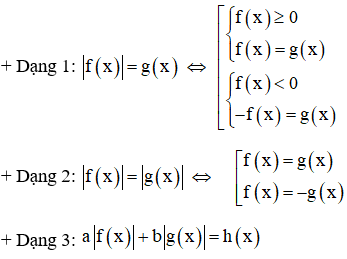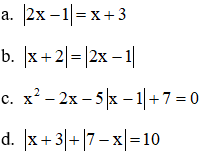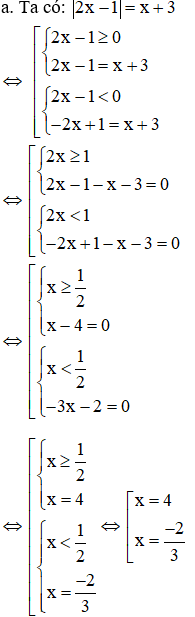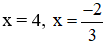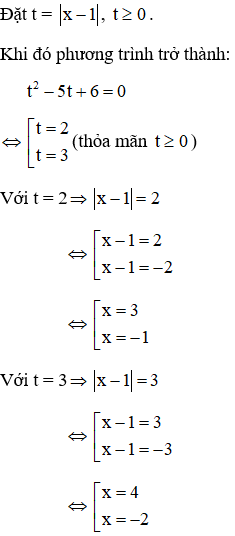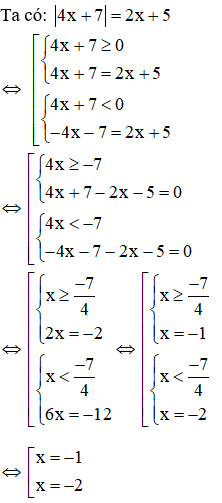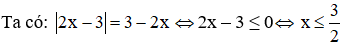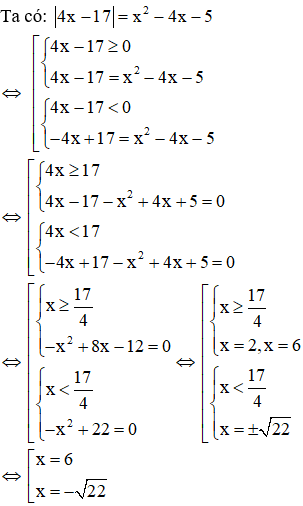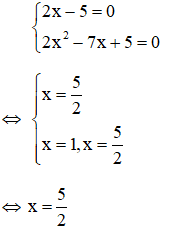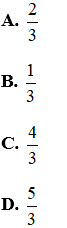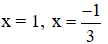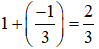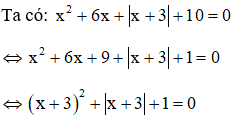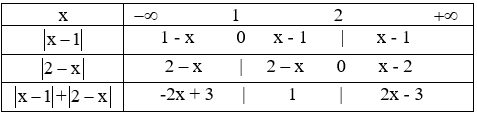Cách giải phương trình có chứa dấu giá trị tuyệt đối hay, chi tiết | Toán lớp 9

Cách giải phương trình có chứa dấu giá trị tuyệt đối hay, chi tiết

Với Cách giải phương trình có chứa dấu giá trị tuyệt đối hay, chi tiết Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình có chứa dấu giá trị tuyệt đối từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta tìm cách khử dấu giá trị tuyệt đối bằng cách:

+ Dùng định nghĩa hoặc tính chất của dấu giá tri tuyệt đối

+ Bình phương hai vế của phương trình

+ Đặt ẩn phụ

Một số dạng phương trình cơ bản

Để giải phương trình này ta thường dùng phương pháp khoảng

Ví dụ: Giải các phương trình sau

Giải

Vậy phương trình có 2 nghiệm

Vậy phương trình có 4 nghiệm x = 3, x = -1, x = 4, x = -2

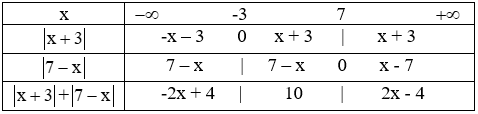
d. Sử dụng định nghĩa dấu giá trị tuyệt đối ta có bảng phá dấu giá trị tuyệt đối sau

Với x < -3 thì phương trình đã cho trở thành -2x + 4 =10 ⇔ -2x = 6 ⇔ x = -3

Ta thấy x = -3 không thỏa mãn điều kiện x < -3 (loại)

Với -3 ≤ x ≤ 7 thì phương trình đã cho trở thành 10 = 10 ⇒ phương trình có vô số nghiệm thỏa mãn -3 ≤ x ≤ 7

Với x > 7 thì phương trình đã cho trở thành 2x - 4 = 10 ⇔ 2x = 14 ⇔ x = 7

Ta thấy x = 7 không thỏa mãn điều kiện x > 7 (loại)

Vậy tập nghiệm của phương trình là S = {x ∈ R: -3 ≤ x ≤ 7}

B. Bài tập

Câu 1: Số nghiệm của phương trình |4x + 7| = 2x + 5 là

A. 0

B. 1

C. 2

D. 3

Giải

Vậy phương trình có 2 nghiệm: x = -1, x = -2

Đáp án C

Câu 2: Số nghiệm của phương trình |2x - 3| = 3 - 2x là

A. 2

B. 3

C. 4

D. vô số nghiệm

Giải

Vậy phương trình có vô số nghiệm

Đáp án D

Câu 3: Nghiệm lớn nhất của phương trình |4x - 17| = x² - 4x - 5 là

A. x = 10

B. x = 8

C. x = 6

D. x = 3

Giải

Vậy nghiệm lớn nhất của phương trình là x = 6

Đáp án C

Câu 4: Biết rằng phương trình |2x - 5| + |2x² - 7x + 5| = 0 có một nghiệm hữu tỉ 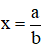, a và b nguyên tố cùng nhau. Tính a + b

A. 4

B. 5

C. 6

D. 7

Giải

Vì |2x - 5| ≥ 0 và |2x² - 7x + 5| ≥ 0 với mọi x nên để |2x - 5| + |2x² - 7x + 5| = 0 thì:

Vậy phương trình có 1 nghiệm là 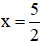. Suy ra a = 5 và b = 2

Vậy a + b = 5 + 2 = 7

Đáp án là D

Câu 5: Tính tổng các nghiệm của phương trình 9x² - 6x-|3x - 1|-1 = 0

Giải

Vậy phương trình có 2 nghiệm:

Suy ra tổng các nghiệm của phương trình là:

Đáp án là A

Câu 6: Tính tích các nghiệm của phương trình x² + 6x + |x + 3| + 10 = 0

Giải

Đặt t = |x + 3|, t ≥ 0. Khi đó phương trình trở thành t² + t + 1 = 0 (*)

Phương trình (*) có ∆ = 1² – 4.1.1 = -3 < 0 nên phương trình vô nghiệm

Vậy phương trình đã cho vô nghiệm

Suy ra không tồn tại tích các nghiệm của phương trình

Đáp án là B

Câu 7: Số nghiệm của phương trình |x - 1| + |2 - x| = 2x là

A. 0

B. 1

C. 2

D. 3

Giải

Sử dụng định nghĩa dấu giá trị tuyệt đối ta có bảng phá dấu giá trị tuyệt đối sau

Với x < 1 thì phương trình đã cho trở thành -2x + 3 = 2x ⇔ 4x = 3 ⇔ x = 3/4

Ta thấy x = 3/4 thỏa mãn điều kiện x < 1 (nhận)

Với 1 ≤ x ≤ 2 thì phương trình đã cho trở thành 1 = 2x ⇔ x = 1/2

Ta thấy x = 1/2 không thỏa mãn điều kiện 1 ≤ x ≤ 2 (loại)

Với x > 2 thì phương trình đã cho trở thành 2x - 3 = 2x ⇔ 0x = -3

Phương trình vô nghiệm

Vậy phương trình có 1 nghiệm x = 3/4

Đáp án B