Các dạng bài tập Toán 9 Chương 3 phần Hình học cực hay có đáp án | Toán lớp 9
Các dạng bài tập Toán 9 Chương 3 phần Hình học cực hay có đáp án
Với Các dạng bài tập Toán 9 Chương 3 phần Hình học cực hay có đáp án Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Chương 3 phần Hình học từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
Lý thuyết & Trắc nghiệm theo bài học
- Lý thuyết Bài 1: Góc ở tâm - Số đo cung (hay, chi tiết)
- Trắc nghiệm Bài 1: Góc ở tâm - Số đo cung
- Lý thuyết Bài 2: Liên hệ giữa cung và dây (hay, chi tiết)
- Trắc nghiệm Bài 2: Liên hệ giữa cung và dây
- Lý thuyết Bài 3: Góc nội tiếp (hay, chi tiết)
- Trắc nghiệm Bài 3: Góc nội tiếp
- Lý thuyết Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung (hay, chi tiết)
- Trắc nghiệm Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
- Lý thuyết Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn (hay, chi tiết)
- Trắc nghiệm Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn
- Lý thuyết Bài 6: Cung chứa góc (hay, chi tiết)
- Trắc nghiệm Bài 6: Cung chứa góc
- Lý thuyết Bài 7: Tứ giác nội tiếp (hay, chi tiết)
- Trắc nghiệm Bài 7: Tứ giác nội tiếp
- Lý thuyết Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp (hay, chi tiết)
- Trắc nghiệm Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp
- Lý thuyết Bài 9: Độ dài đường tròn, cung tròn (hay, chi tiết)
- Trắc nghiệm Bài 9: Độ dài đường tròn, cung tròn
- Lý thuyết Bài 10: Diện tích hình tròn, hình quạt tròn (hay, chi tiết)
- Trắc nghiệm Bài 10: Diện tích hình tròn, hình quạt tròn
- Tổng hợp lý thuyết Chương 3 Hình học 9 (hay, chi tiết)
- Tổng hợp Trắc nghiệm Chương 3 Hình học 9
Các dạng bài tập
- Cách tính số đo góc ở tâm và số đo cung bị chắn cực hay, chi tiết
- Cách giải bài tập Liên hệ giữa cung và dây cực hay, chi tiết
- Các dạng bài tập về Góc nội tiếp chọn lọc, có lời giải
- Cách tính số đo góc nội tiếp cực hay, chi tiết
- Cách giải bài tập Góc tạo bởi tia tiếp tuyến và dây cung cực hay, chi tiết
- Cách chứng minh tiếp tuyến của một đường tròn cực hay, chi tiết
- Cách chứng minh hai góc hoặc hai đoạn thẳng bằng nhau cực hay, chi tiết
- Cách chứng minh hai đường thẳng vuông góc cực hay, chi tiết
- Cách giải bài tập Quỹ tích cung chứa góc cực hay, chi tiết
- Cách chứng minh nhiều điểm cùng thuộc một đường tròn cực hay
- Cách dựng cung chứa góc cực hay, chi tiết
- Cách chứng minh tứ giác nội tiếp cực hay, chi tiết
- Ứng dụng của tứ giác nội tiếp chứng minh song song, vuông góc, thẳng hàng, đồng quy
- Cách xác định tâm và bán kính đường tròn ngoại tiếp, đường tròn nội tiếp
- Tính các đại lượng liên quan đến đa giác ngoại tiếp, nội tiếp đường tròn
- Cách tính độ dài đường tròn, cung tròn cực hay, chi tiết
- Tính số đo cung do nhiều cung tạo thành và so sánh độ dài hai cung
- Cách tính diện tích hình tròn, hình quạt tròn cực hay, chi tiết
- Tính diện tích các hình liên quan đến diện tích hình tròn, hình quạt tròn
Lý thuyết Góc ở tâm. Số đo cung
1. Góc ở tâm
Góc có đỉnh trùng với tâm của đường tròn được gọi là góc ở tâm.
+ Hai cạnh của góc ở tâm cắt đường tròn tại hai điểm, do đó chia đường tròn thành hai cung.
⋅ Với các góc α ( 0 < α < 180°) thì cung nằm bên trong góc được gọi là cung nhỏ.
⋅ Cung nằm bên ngoài góc được gọi là cung lớn.
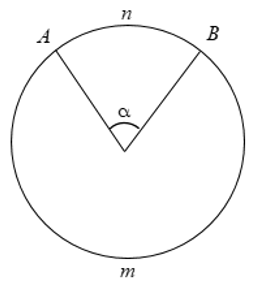
+ Cung AB được kí hiệu là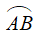 
.
+ Cung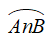 
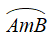
là cung nhỏ, cung 
là cung lớn.
+ Với α = 180° thì mỗi cung là một nửa đường tròn.
+ Cung nằm bên trong góc gọi là cung bị chắn.
+ Cung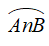 
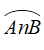
là cung bị chắn bởi góc AOB hay góc AOB chắn cung nhỏ 
.
2. Số đo cung.
+ Số đo của cung nhỏ bằng số đo góc ở tâm chắn cung đó.
+ Số đo của cung lớn bằng hiệu giữa 360° và số đo cung nhỏ (có chung hai mút với cung lớn).
+ Số đo của nửa đường tròn bằng 180°
+ Kí hiệu số đo của cung AB là sđ .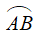
Ví dụ: Cho góc α = 100° là góc ở tâm O như hình vẽ. Tính số đo cung lớn.
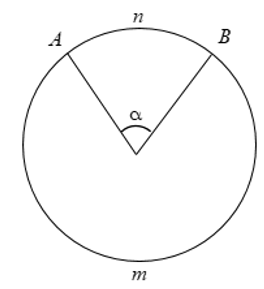
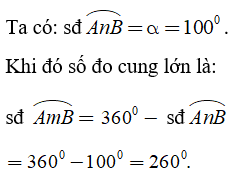
Chú ý:
+ Cung nhỏ có số đo nhỏ hơn 180°
+ Cung lớn có số đo lớn hơn 180°
+ Khi hai mút của cung trùng nhau, ta có “cung không” với số đo là 0° và cả đường tròn có số đo là 360°
3. So sánh hai cung.
+ Hai cung được gọi là bằng nhau nếu chúng có cùng số đo bằng nhau.
+ Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.
+ Kí hiệu: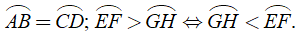 
4. Khi nào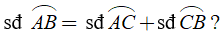
Nếu C là một điểm nằm trên cung AB thì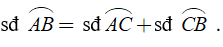
B. Bài tập tự luận
Câu 1: Cho hình vẽ sau:
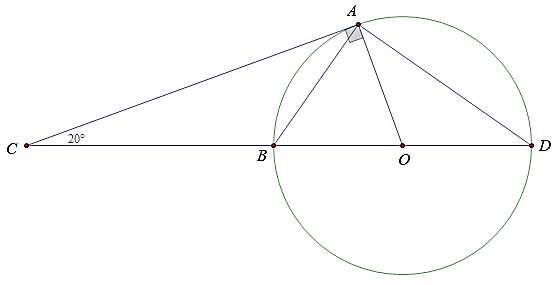
Tính số đo cung nhỏ AB,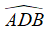 
từ đó so sánh cạnh AC và AD
Lời giải:
Ta có:
Câu 2: Dựa vào hình dưới, hình tính số đo của cung nhỏ AB, biết rằng B là trung điểm của OC
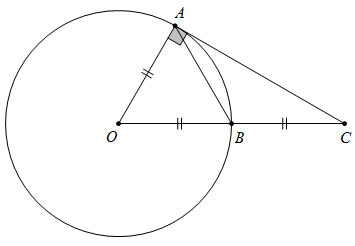
Lời giải:
Ta có tam giác ABC vuông tại A có B là trung điểm của OC
Suy ra OB = BC = AB
Mà OB = OA suy ra OB = OA = AB
Khi đó Δ OAB đều nên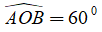 
⇒ Số đo cung nhỏ AB bằng 60°
Liên hệ giữa cung và dây: lý thuyết, các dạng bài tập có đáp án
1. Định lí 1
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+ Hai cung bằng nhau căng hai dây bằng nhau.
+ Hai dây bằng nhau căng hai cung bằng nhau.
2. Định lí 2
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+ Cung lớn hơn căng dây lớn hơn.
+ Dây lớn hơn căng cung lớn hơn.
3. Bổ sung
+ Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
+ Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
+ Trong một đường tròn, đường kính đi qua trung điểm của một dây (không đi qua tâm) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
+ Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
4. Ví dụ cụ thể
Câu 1: Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O). Biết ∠A = 50°, hãy so sánh các cung nhỏ AB, AC và BC.
Hướng dẫn:
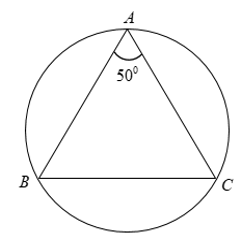
Ta có: ΔABC cân tại A và ∠A = 50°
Khi đó
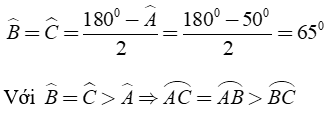
B. Bài tập tự luận
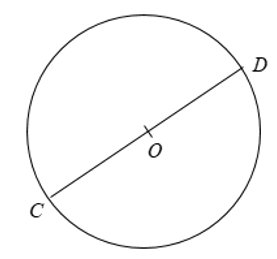
Bài 1: Dựa vào hình vẽ sau, hãy so sánh AB và CD:
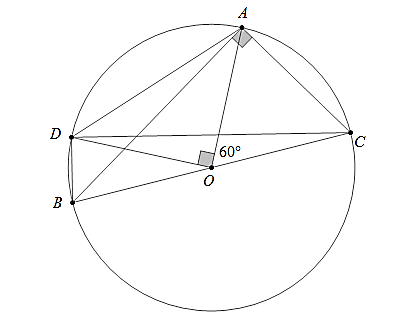
Lời giải:
Ta có:
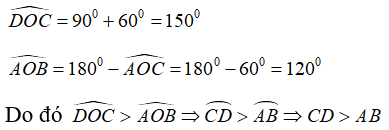
Bài 2: Cho (O) có dây cung BC cố định. Gọi A là điểm thuộc cung lớn BC sao cho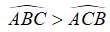 
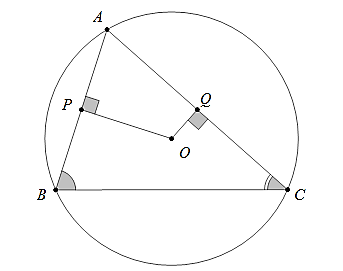
. Chứng minh rằng khoảng cách từ O đến AB lớn hơn khoảng cách từ O đến AC.
Lời giải:
Gọi P, Q lần lượt là chân đường cao hạ từ O đến AB, AC. Ta sẽ chứng minh:
