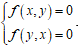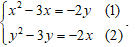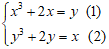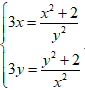Cách giải hệ phương trình đối xứng loại 2 cực hay | Toán lớp 9
Cách giải hệ phương trình đối xứng loại 2 cực hay
Với Cách giải hệ phương trình đối xứng loại 2 cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải hệ phương trình đối xứng loại 2 từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
A. Phương pháp giải
Hệ phương trình đối xứng loại II theo ẩn x và y là hệ phương trình mà khi ta đổi vai trò của các ẩn x và y thì hai phương trình trong hệ sẽ hoán đổi cho nhau.
Hệ phương trình đối xứng loại II có dạng 
Bước 1: Cộng hoặc trừ hai vế của hai hệ phương trình thu được phương trình. Biến đổi phương trình này về phương trình tích, tìm biểu thức liên hệ giữa x và y đơn giản.
Bước 2: Thế x theo y (hoặc y theo x) vào một trong hai phương trình của hệ ban đầu.
Bước 3: Giải và tìm ra nghiệm x (hoặc y). Từ đó suy ra nghiệm còn lại.
Bước 4: Kết luận nghiệm của hệ phương trình.
B. Ví dụ minh họa
Ví dụ 1: Giải hệ phương trình 
Hướng dẫn:
Trừ từng vế của hai phương trình ta được:
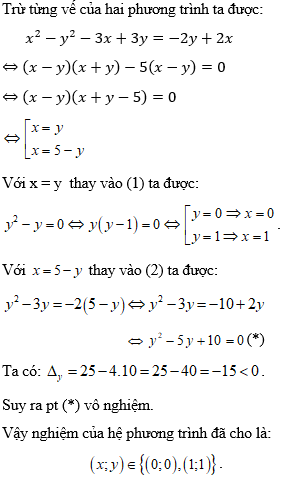
Ví dụ 2: Giải hệ phương trình 
Hướng dẫn:
Trừ từng vế của hai phương trình ta được:
Ví dụ 3: Giải hệ phương trình 
Hướng dẫn:
Vì vế phải của mỗi phương trình đều dương nên ta có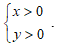 
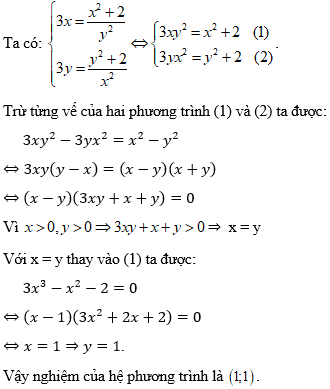
C. Bài tập trắc nghiệm
Câu 1: Hệ phương trình sau có bao nhiêu nghiệm: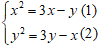 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
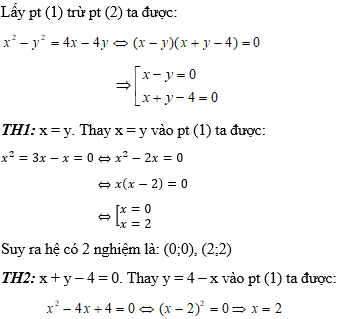
Với x = 2 ⇒ y = 2. Suy ra hệ có nghiệm là: (2;2)
Vậy hệ phương trình có 2 nghiệm là: (0;0), (2;2).
Chọn đáp án B.
Câu 2: Hệ phương trình sau có bao nhiêu nghiệm: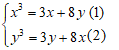 
A. 4
B. 2
C. 3
D. 5
Lời giải:
Hướng dẫn:
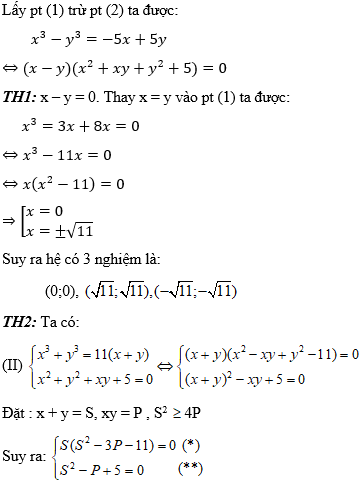
Chọn đáp án C.
Câu 3: Hệ phương trình sau có bao nhiêu nghiệm: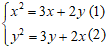 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
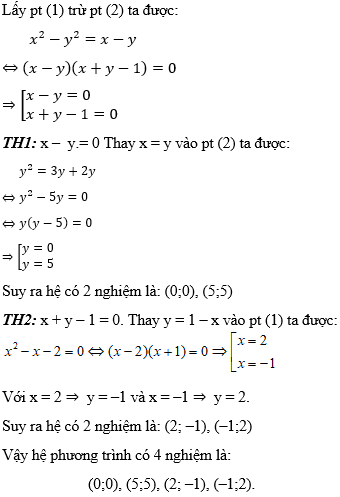
Chọn đáp án D.
Câu 4: Hệ phương trình sau có bao nhiêu nghiệm: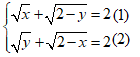 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
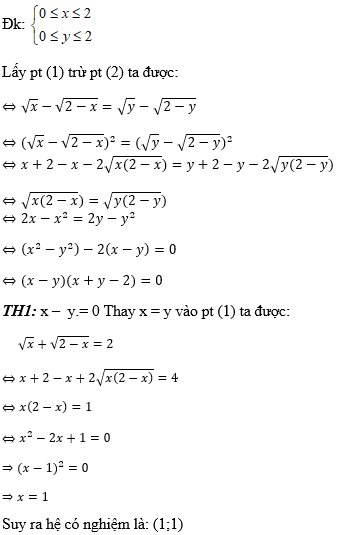
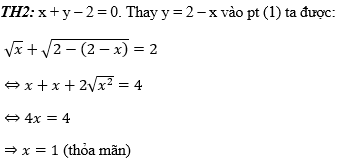
Với x = 1 ⇒ y = 1. Suy ra hệ có nghiệm là: (1; 1),
Vậy hệ phương trình có 1 nghiệm là: (1;1).
Chọn đáp án A.
Câu 5: Hệ phương trình sau có bao nhiêu nghiệm: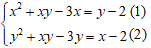 
A. 4
B. 3
C. vô số nghiệm
D. vô nghiệm
Lời giải:
Hướng dẫn:
Lấy pt (1) trừ pt (2) ta được:
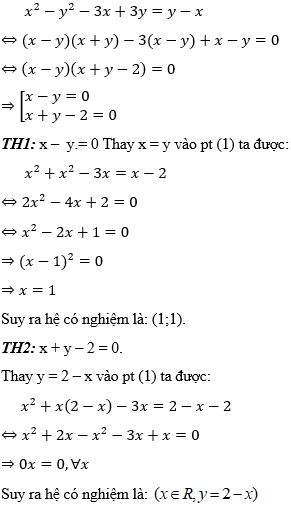
Vậy hệ phương trình có vô số nghiệm là: (x ∈ R, y = 2 - x).
Chọn đáp án C.
Câu 6: Hệ phương trình sau: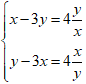 
. Khẳng định nào sau đây đúng ?
A. Hệ phương trình có vô số nghiệm.
B. Hệ phương trình có 3 nghiệm.
C. Hệ phương trình có 4 nghiệm.
D. Hệ phương trình có 1 nghiệm.
Lời giải:
Hướng dẫn:
Đk: x ≠ 0, y ≠ 0
Lấy pt (1) trừ pt (2) ta được:
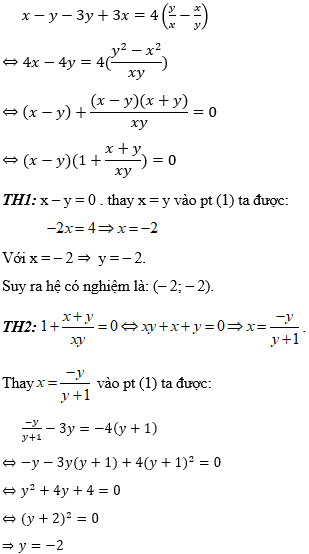
Với y = –2 ⇒ x = –2 (tm). Suy ra hệ có nghiệm là: (– 2; – 2).
Vậy hệ phương trình có 1 nghiệm là: (– 2; – 2).
Chọn đáp án D.
Câu 7: Hệ phương trình sau: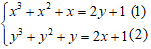 
. Khẳng định nào sau đây đúng ?
A. Hệ phương trình có vô số nghiệm.
B. Hệ phương trình có 2 nghiệm.
C. Hệ phương trình có 4 nghiệm.
D. Hệ phương trình có 3 nghiệm.
Lời giải:
Hướng dẫn:
Lấy pt (1) trừ pt (2) ta được:
x3 - y3 + x2 - y2 + x - y = 2y - 2x
⇔ (x - y)(x2 + xy + y2 ) + (x - y)(x + y) + 3(x - y) = 0
⇔ (x - y)(x2 + y2 + xy + x + y + 3) = 0
TH1: x – y = 0 . thay x = y vào pt (1) ta được:
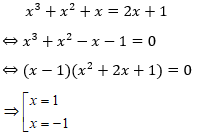
Với x = – 1 ⇒ y = – 1 và x = 1 ⇒ y = 1. Suy ra hệ có 2 nghiệm là: (– 1; – 1), (1;1).
TH2: x2 + y2 + xy + x + y + 3 = 0 ⇔ x2 + (y + 1)x + y2 + y + 3 = 0 (3)
Ta có: △x = (y + 1)2 - 4(y2 + y + 3) = y2 + 2y + 1 - 4y2 - 4y - 12 = -(3y2 + 2y + 11) (*)
Tính: Δy' = 1 - 33 = -32 < 0. Suy ra pt (*) vô nghiệm.
Suy ra pt (3) vô nghiệm.
Vậy hệ phương trình có 2 nghiệm là: (– 1; – 1), (1;1).
Chọn đáp án B.
Câu 8: Hệ phương trình sau: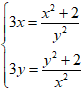 
. Khẳng định nào sau đây đúng?
A. Hệ phương trình vô nghiệm.
B. Hệ phương trình có 2 nghiệm.
C. Hệ phương trình có 1 nghiệm.
D. Hệ phương trình có 3 nghiệm
Lời giải:
Hướng dẫn:
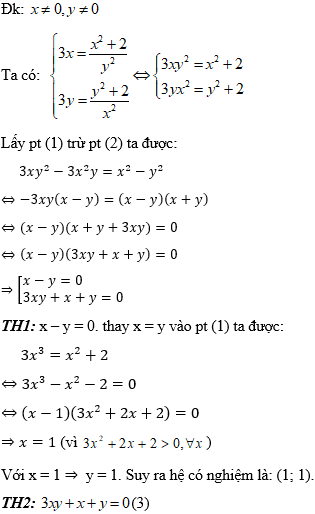
Từ hệ phương trình ta thấy, x > 0, y > 0 ⇒ x + y + 3xy > 0. Vậy phương trình (3) vô nghiệm.
Vậy hệ phương trình có 1 nghiệm là: (1; 1).
Chọn đáp án C.
Câu 9: Hệ phương trình sau có bao nhiêu nghiệm: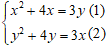 
A. 2
B. 3
C. vô số nghiệm
D. vô nghiệm
Lời giải:
Hướng dẫn:
Lấy pt (1) trừ pt (2) ta được:
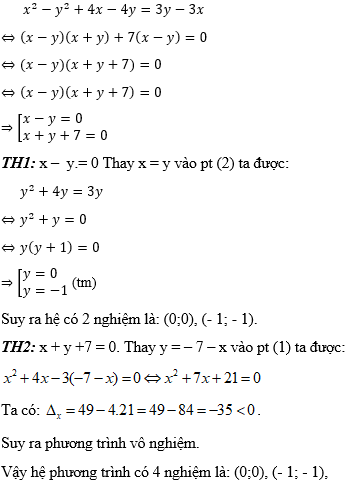
Chọn đáp án A.
Câu 10: Hệ phương trình sau có bao nhiêu nghiệm: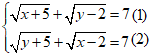 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
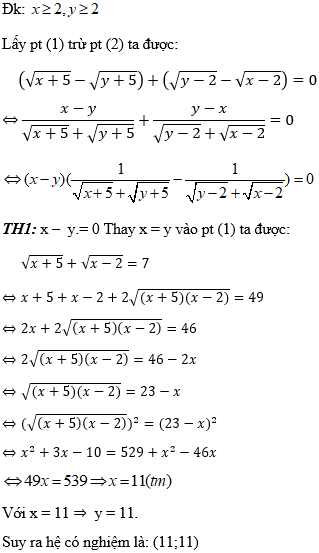
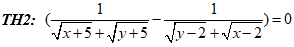
Vì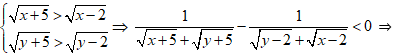 
phương trình vô nghiệm.
Vậy hệ phương trình có 1 nghiệm là: (11;11).
Chọn đáp án A.
