Lý thuyết Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết | Toán lớp 9

Lý thuyết Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết

Tài liệu Lý thuyết Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Biến đổi đơn giản biểu thức chứa căn thức bậc hai từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

A. Lý thuyết

I. BIẾN ĐỔI BIỂU THỨC ĐƠN GIẢN CHỨA CĂN BẬC HAI

a) Đưa một thừa số ra ngoài dấu căn

Với hai biểu thức A, B mà B ≥ 0 ta có

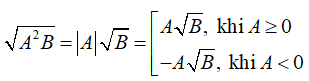
Ví dụ:

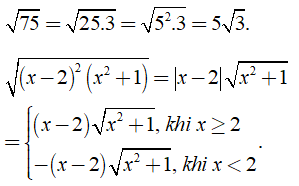
b) Đưa thừa số vào trong dấu căn

Với A ≥ 0, B ≥ 0 thì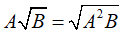

Với A < 0, B ≥ 0 thì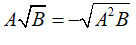

Ví dụ:

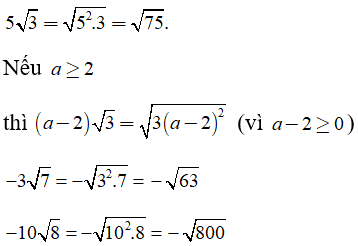
c) Khử mẫu của biểu thức dưới dấu căn.

Với AB ≥ 0 và B ≠ 0 thì

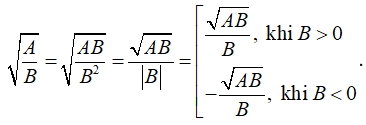
Ví dụ:

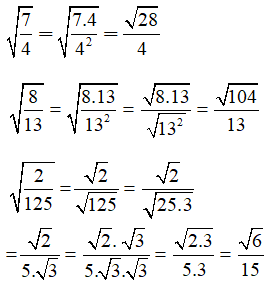
d) Trục căn thức ở mẫu

Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số

    • Với các biểu thức A, B mà B > 0 ta có: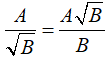

Ví dụ:

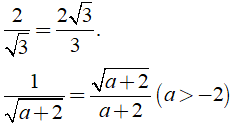
    • Với các biểu thức A, B, C mà A ≥ 0, A ≠ B², ta có:

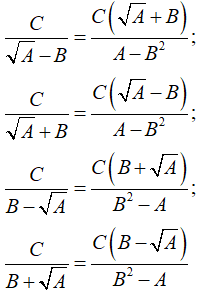
Ví dụ:

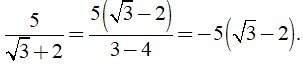
    • Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:

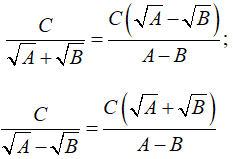
Ví dụ:

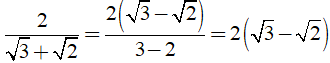
II. RÚT GỌN BIỂU THỨC CHỨA CĂN BẬC HAI

- Để rút gọn biểu thức chứa căn bậc hai, ta cần vận dụng phối hợp các phép tính và các phép biến đổi đã biết.

- Khi rút gọn một dãy các phép tính cộng, trừ, nhân, chia, lũy thứa và khai phương thì thứ tự thực hiện: khai căn trước rồi đến lũy thừa, sau đó đến nhân, chia, cộng, trừ

B. Bài tập tự luận

Câu 1: Cho biểu thức

(với x ≥ 0; x ≠ 1 và x ≠ 1/4).

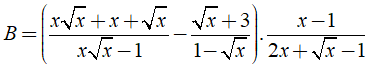
Tìm tất cả các giá trị của x để B < 0.

Lời giải:

Ta có:

(với x ≥ 0; x ≠ 1 và x ≠ 1/4).

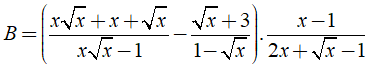
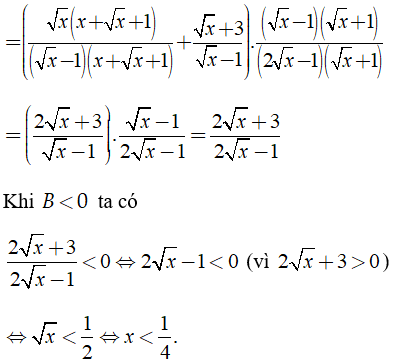
Kết hợp điều kiện ta có x ∈ [0; 1/4].

Câu 2: Giải các phương trình sau:

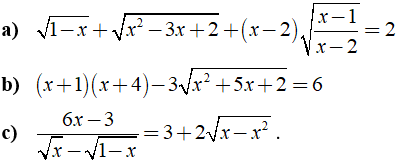
Lời giải:

a) Điều kiện xác định:

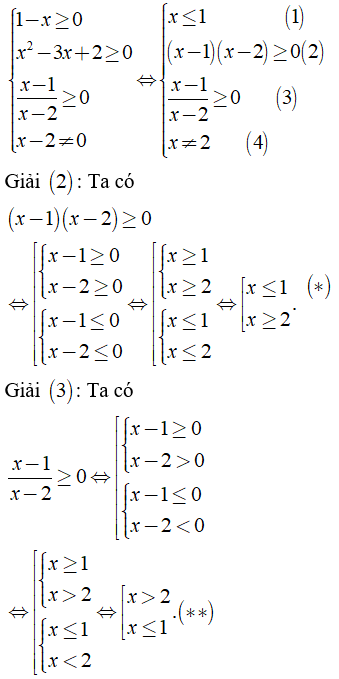
Kết hợp (1), (4), (*) và (**) ta có điều kiện xác định: x ≤ 1

Ta có:

b) Điều kiện xác định: .

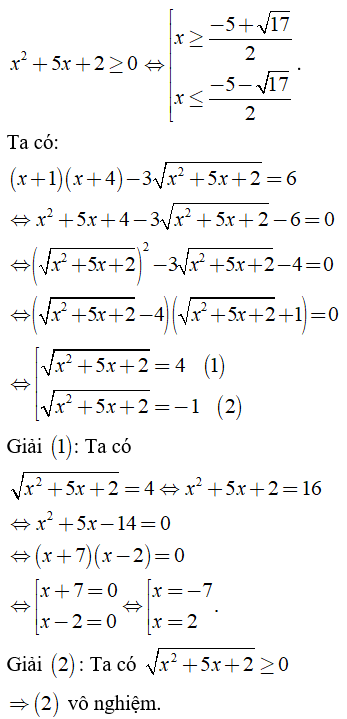
So sánh điều kiện ta có: x = -7; x = 2 (t/m). Vậy S = {-7; 2}.

c) Điều kiện xác định x ∈ [0; 1]\{1/2}.

Ta có:

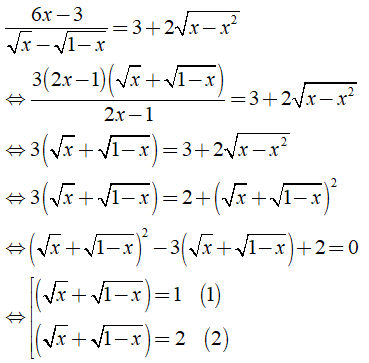
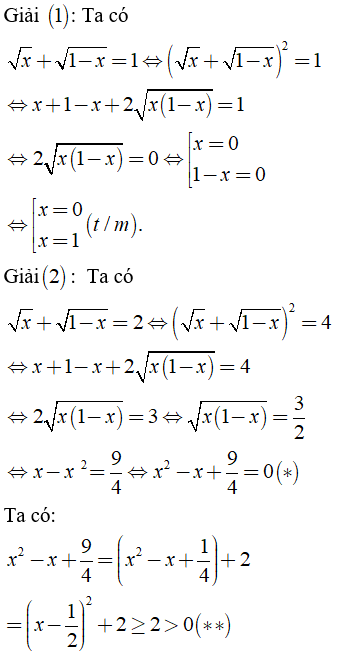
Từ (*) và (**) suy ra phương trình (2) vô nghiệm.

Vậy S = {0; 1}.

Câu 3: Rút gọn các biểu thức sau:

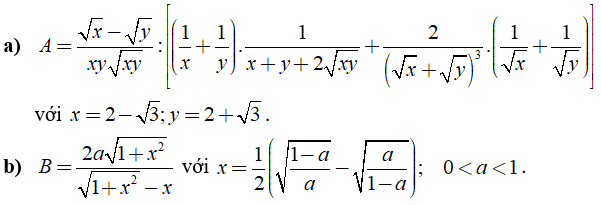
Lời giải:

a) Ta có:

b) Ta có

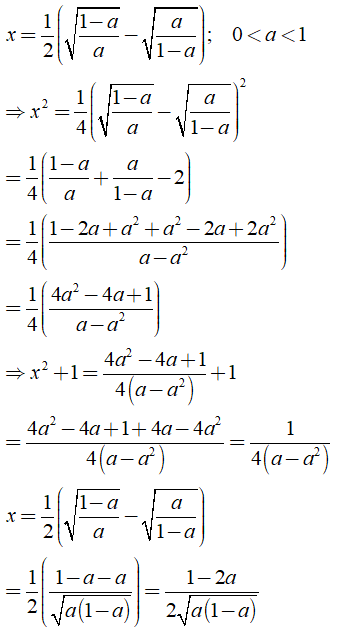
Khi đó: .

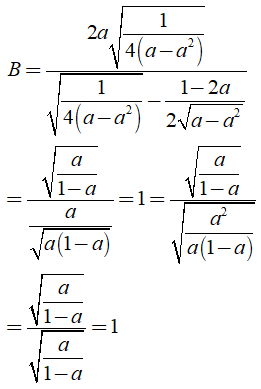
Câu 4: Chứng minh rằng

(n ∈ N; n ≥ 2)

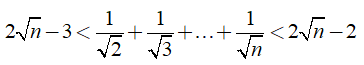
Lời giải: